
A stochastic process is a collection of random variables that are indexed by some mathematical sets. That is, each random variable of the stochastic process is uniquely associated with an element in the set. The set that is used to index the random variables is called the index set and the set of random variables forms the state space. A stochastic process can be classified in many ways based on state space, index set, etc.
When the stochastic process is interpreted as time, if the process has a finite number of elements such as integers, numbers, and natural numbers then it is Discrete Time.
Stochastic Model
It is a discrete-time process indexed at time 1,2,3,…that takes values called states which are observed.
For an example if the states (S) ={hot , cold }
State series over time => z∈ S_T
Weather for 4 days can be a sequence => {z1=hot, z2 =cold, z3 =cold, z4 =hot}
Markov and Hidden Markov models are engineered to handle data which can be represented as ‘sequence’ of observations over time. Hidden Markov models are probabilistic frameworks where the observed data are modeled as a series of outputs generated by one of several (hidden) internal states.
Markov Assumptions
Markov models are developed based on mainly two assumptions.
- Limited Horizon assumption: Probability of being in a state at a time t depend only on the state at the time (t-1).

Eq.1. Limited Horizon Assumption
That means state at time t represents enough summary of the past reasonably to predict the future. This assumption is an Order-1 Markov process. An order-k Markov process assumes conditional independence of state z_t from the states that are k + 1-time steps before it.
2. Stationary Process Assumption: Conditional (probability) distribution over the next state, given the current state, doesn't change over time.
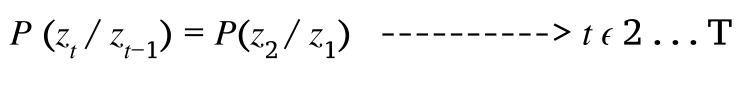
Eq.2. Stationary Process Assumption
That means states keep on changing over time but the underlying process is stationary.
Notation Convention
There is an initial state and an initial observation z_0 = s_0
s_0 — initial probability distribution over states at time 0.
Initial state probability — (π)
at t=1, probability of seeing first real state z_1 is p(z_1/z_0)
Since z0 = s0 ,

State Transition Matrix

𝐀𝐢,𝐣= probability of transitioning from state i to state j at any time t. Following is a State Transition Matrix of four states including the initial state.

Fig.2. State Transition Matrix —Image by Author
Two Main Questions in Markov-model
Probability of particular sequences of state z?
How do we estimate the parameter of state transition matrix A to maximize the likelihood of the observed sequence?
Probability of particular sequences

Eq.4. Finding probability of particular sequence
Consider the state transition matrix above(Fig.2.) and lets find out the probability of sequence — > {z1 = s_hot , z2 = s_cold , z3 = s_rain , z4 = s_rain , z5 = s_cold}
P(z) = P(s_hot|s_0 ) P(s_cold|s_hot) P(s_rain|s_cold) P(s_rain|s_rain) P(s_cold|s_rain)
\= 0.33 x 0.1 x 0.2 x 0.7 x 0.2 = 0.000924
Hidden Markov Model (HMM)
When we can not observe the state themselves but only the result of some probability function(observation) of the states we utilize HMM. HMM is a statistical Markov model in which the system being modeled is assumed to be a Markov process with unobserved (hidden) states.
Markov Model*: Series of (hidden) states z={z_1,z_2………….} drawn from state alphabet S ={s_1,s_2,…….𝑠_|𝑆|} where z_i belongs to S.*
Hidden Markov Model*: Series of observed output x = {x_1,x_2,………} drawn from an output alphabet V= {𝑣1, 𝑣2, . . , 𝑣_|𝑣|} where x_i belongs to V*
Assumptions of HMM
HMM too is built upon several assumptions and the following is vital.
- Output independence assumption: Output observation is conditionally independent of all other hidden states and all other observations when given the current hidden state.

Eq.5.
- Emission Probability Matrix: Probability of hidden state generating output v_i given that state at the corresponding time was s_j.
Hidden Markov Model as a finite state machine
Consider the example given below in Fig.3. which elaborates how a person feels on different climates.

Fig.3. Markov Model as Finite State Machine — Image by Author
Set of states (S) = {Happy, Grumpy}
Set of hidden states (Q) = {Sunny , Rainy}
State series over time = z∈ S_T
Observed States for four day = {z1=Happy, z2= Grumpy, z3=Grumpy, z4=Happy}
The feeling that you understand from a person emoting is called the observations since you observe them.
The weather that influences the feeling of a person is called the hidden state since you can’t observe it.
Emission probabilities
In the above example, feelings (Happy or Grumpy) can be only observed. A person can observe that a person has an 80% chance to be Happy given that the climate at the particular point of observation( or rather day in this case) is Sunny. Similarly the 60% chance of a person being Grumpy given that the climate is Rainy. Here mentioned 80% and 60% are Emission probabilities since they deal with observations.
Transition probabilities
When we consider the climates (hidden states) that influence the observations there are correlations between consecutive days being Sunny or alternate days being Rainy. There is 80% for the Sunny climate to be in successive days whereas 60% chance for consecutive days being Rainy. The probabilities that explain the transition to/from hidden states are Transition probabilities.
Three important questions in HMM are
What is the probability of an observed sequence?
What is the most likely series of states to generate an observed sequence?
How can we learn the values for the HMMs parameters A and B given some data?
1. Probability of Observed Sequence
We have to add up the likelihood of the data x given every possible series of hidden states. This will lead to a complexity of O(|S|)^T. Hence two alternate procedures were introduced to find the probability of an observed sequence.
- Forward Procedure
Calculate the total probability of all the observations (from t_1 ) up to time t.
𝛼_𝑖 (𝑡) = 𝑃(𝑥_1 , 𝑥_2 , … , 𝑥_𝑡, 𝑧_𝑡 = 𝑠_𝑖; 𝐴, 𝐵)
- Backward Procedure
Similarly calculate total probability of all the observations from final time (T) to t.
𝛽_i (t) = P(x_T , x_T-1 , …, x_t+1 , z_t= s_i ; A, B)
Example using forward procedure
S = {hot,cold}
v = {v1=1 ice cream ,v2=2 ice cream,v3=3 ice cream} where V is the Number of ice creams consumed on a day.
Example Sequence = {x1=v2,x2=v3,x3=v1,x4=v2}

Fig.4. Given data as matrices — Image by Author

Fig.5. Generated Finite state machines for HMM — Image by Author
We first need to calculate the prior probabilities (that is, the probability of being hot or cold previous to any actual observation). This can be obtained from S_0 or π. From Fig.4. S_0 is provided as 0.6 and 0.4 which are the prior probabilities. Then based on Markov and HMM assumptions we follow the steps in figures Fig.6, Fig.7. and Fig.8. below to calculate the probability of a given sequence.
1. For first observed output x1=v2

Fig.6. Step 1 — Image by Author
2. for observed output x2=v3

Fig.7. Step 2 — Image by Author
3. for observed output x3 and x4
Similarly for x3=v1 and x4=v2, we have to simply multiply the paths that lead to v1 and v2.

Fig.8. Step 3 and 4 —Image by Author
2. Maximum likelihood assignment
For a given observed sequence of outputs 𝑥 𝜖 𝑉_𝑇, we intend to find the most likely series of states 𝑧 𝜖 𝑆_𝑇. We can understand this with an example found below.

Fig.9. Data for example 2 — Image by Author

Fig.10. Markov Model as a Finite State Machine from Fig.9. data —Image by Author
The Viterbi algorithm is a dynamic programming algorithm similar to the forward procedure which is often used to find maximum likelihood. Instead of tracking the total probability of generating the observations, it tracks the maximum probability and the corresponding state sequence.
Consider the sequence of emotions : H,H,G,G,G,H for 6 consecutive days. Using the Viterbi algorithm we will find out the more likelihood of the series.

Fig.11. The Viterbi algorithm requires to choose the best path —Image by Author
There will be several paths that will lead to sunny for Saturday and many paths that lead to Rainy Saturday. Here we intend to identify the best path up-to Sunny or Rainy Saturday and multiply with the transition emission probability of Happy (since Saturday makes the person feels Happy).
Let's consider A sunny Saturday. The previous day(Friday) can be sunny or rainy. Then we need to know the best path up-to Friday and then multiply with emission probabilities that lead to grumpy feeling. Iteratively we need to figure out the best path at each day ending up in more likelihood of the series of days.

Fig.12. Step-1 — Image by Author

Fig.13. Step-2 — Image by Author

Fig.14. Iterate the algorithm to choose the best path — Image by Author
The algorithm leaves you with maximum likelihood values and we now can produce the sequence with a maximum likelihood for a given output sequence.
3. Learn the values for the HMMs parameters A and B
Learning in HMMs involves estimating the state transition probabilities A and the output emission probabilities B that make an observed sequence most likely. Expectation-Maximization algorithms are used for this purpose. An algorithm is known as Baum-Welch algorithm, that falls under this category and uses the forward algorithm, is widely used.
The blog comprehensively describes Markov and HMM. The blog is mainly intended to provide an explanation with an example to find the probability of a given sequence and maximum likelihood for HMM which is often questionable in examinations too. Thanks for reading the blog up to this point and hope this helps in preparing for the exams.
